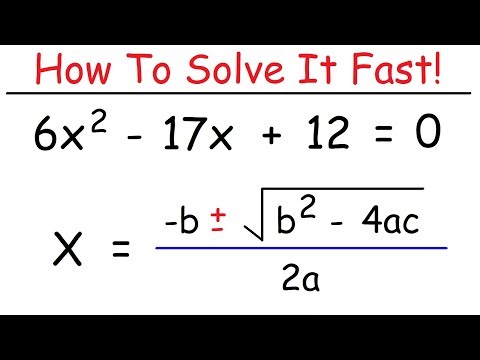
Isi
Persamaan kuadrat adalah persamaan yang berisi variabel tunggal dan di mana variabel kuadrat. Bentuk standar untuk jenis persamaan ini, yang selalu menghasilkan parabola saat digambarkan, adalah kapak2 + bx + c = 0, dimana Sebuah, b dan c adalah konstanta. Menemukan solusi tidak semudah seperti untuk persamaan linear, dan sebagian alasannya adalah bahwa, karena istilah kuadrat, selalu ada dua solusi. Anda bisa menggunakan salah satu dari tiga metode untuk menyelesaikan persamaan kuadrat. Anda bisa memfaktorkan istilah, yang paling cocok dengan persamaan yang lebih sederhana, atau Anda bisa menyelesaikan kuadrat. Metode ketiga adalah dengan menggunakan rumus kuadrat, yang merupakan solusi umum untuk setiap persamaan kuadratik.
Formula Quadratic
Untuk persamaan kuadrat umum dari formulir kapak2 + bx + c = 0, solusi diberikan oleh rumus ini:
x = ÷ 2_a_
Perhatikan bahwa tanda ± di dalam tanda kurung berarti selalu ada dua solusi. Salah satu solusi menggunakan ÷ 2_a_, dan solusi lainnya menggunakan ÷ 2_a_.
Menggunakan Formula Quadratic
Sebelum Anda dapat menggunakan rumus kuadrat, Anda harus memastikan persamaan dalam bentuk standar. Mungkin tidak. Beberapa x2 istilah mungkin ada di kedua sisi persamaan, jadi Anda harus mengumpulkan yang di sisi kanan. Lakukan hal yang sama dengan semua x syarat dan konstanta.
Contoh: Temukan solusi untuk persamaan 3_x_2 - 12 = 2_x_ (x -1).
Luaskan braket:
3_x_2 - 12 = 2_x_2 - 2_x_
Kurangi 2_x_2 dan dari kedua sisi. Tambahkan 2_x_ ke kedua sisi
3_x_2 - 2_x_2 + 2_x_ - 12 = 2_x_2 -2_x_2 -2_x_ + 2_x_
3_x_2 - 2_x_2 + 2_x_ - 12 = 0
x2 - 2_x_ -12 = 0
Persamaan ini dalam bentuk standar kapak2 + bx + c = 0 di mana Sebuah = 1, b = −2 dan c = 12
Rumus kuadratik adalah
x = ÷ 2_a_
Sejak Sebuah = 1, b = −2 dan c = −12, ini menjadi
x = ÷ 2(1)
x = ÷ 2.
x = ÷ 2
x = ÷ 2
x = 9,21 ÷ 2 dan x = −5.21 ÷ 2
x = 4.605 dan x = −2.605
Dua Cara Lain untuk Memecahkan Persamaan Kuadrat
Anda dapat memecahkan persamaan kuadrat dengan memfaktorkan. Untuk melakukan ini, Anda kira-kira kira-kira pada angka yang, ketika ditambahkan bersama, memberikan konstanta b dan, ketika dikalikan bersama, berikan konstanta c. Metode ini bisa sulit ketika fraksi terlibat. dan tidak akan bekerja dengan baik untuk contoh di atas.
Metode lainnya adalah menyelesaikan kuadrat. Jika Anda memiliki persamaan adalah bentuk standar, kapak2 + bx + c = 0, masukkan c di sisi kanan dan tambahkan istilah (b/2)2 ke kedua sisi. Ini memungkinkan Anda untuk mengekspresikan sisi kiri sebagai (x + d)2dimana d adalah konstan. Anda kemudian dapat mengambil akar kuadrat dari kedua sisi dan menyelesaikannya x. Sekali lagi, persamaan dalam contoh di atas lebih mudah untuk diselesaikan dengan menggunakan rumus kuadratik.