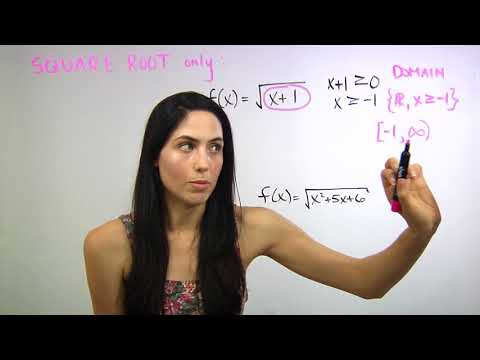
Domain fraksi mengacu pada semua bilangan real yang dapat variabel independen dalam fraksi. Mengetahui kebenaran matematika tertentu tentang bilangan real dan menyelesaikan beberapa persamaan aljabar sederhana dapat membantu Anda menemukan domain dari ekspresi rasional apa pun.
Lihatlah penyebut fraksi. Penyebutnya adalah angka terbawah dalam fraksi. Karena tidak mungkin untuk membagi dengan nol, penyebut fraksi tidak dapat sama dengan nol. Oleh karena itu, untuk fraksi 1 / x, domainnya adalah "semua angka tidak sama dengan nol," karena penyebut tidak dapat sama dengan nol.
Cari akar kuadrat di mana saja dalam masalah, misalnya (sqrt x) / 2. Karena akar kuadrat dari angka negatif tidak nyata, nilai-nilai di bawah simbol akar kuadrat harus lebih besar dari atau sama dengan nol. Dalam contoh masalah kami, domainnya adalah "semua angka lebih besar dari atau sama dengan nol."
Buat masalah aljabar untuk mengisolasi variabel dalam fraksi yang lebih rumit.
Misalnya: Untuk menemukan domain 1 / (x ^ 2 -1), atur masalah aljabar untuk menemukan nilai x yang akan menyebabkan penyebutnya sama dengan 0. X ^ 2-1 = 0 X ^ 2 = 1 Sqrt (x ^ 2) = Sqrt 1 X = 1 atau -1. Domainnya adalah "semua angka tidak sama dengan 1 atau -1."
Untuk menemukan domain (sqrt (x-2)) / 2, atur masalah aljabar untuk menemukan nilai x yang akan menyebabkan nilai di bawah simbol akar kuadrat kurang dari 0. x-2 <0 x < 2 Domain adalah "semua angka lebih besar dari atau sama dengan 2."
Untuk menemukan domain 2 / (sqrt (x-2)), atur masalah aljabar untuk menemukan nilai x yang akan menyebabkan nilai di bawah simbol akar kuadrat menjadi kurang dari 0 dan nilai x yang akan menyebabkan penyebut sama dengan 0.
x-2 <0 x-2 <0 x <2
dan
Sqrt (x-2) = 0 (sqrt (x-2)) ^ 2 = 0 ^ 2 x-2 = 0 x = 2
Domain adalah "semua angka lebih besar dari 2."